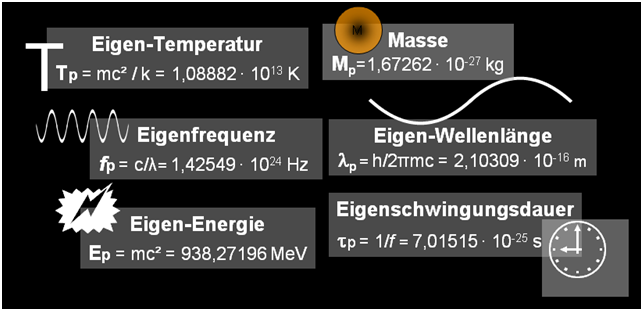
Die Eigenschwingung des Protons erzeugt aufgrund seiner Superstabilität innerhalb der Materie sich-selbst-ähnliche Strukturen – Fraktale.
ARTE zeigte folgenden Film über Benoit Mandelbrot, als ein Begründer der fraktalen Geometrie:
Mandelbrot arbeitete nach dem 2.Weltkrieg bei IBM. Dort erzählten ihm die Kollegen vom einem Datenübertragungsproblem. Daten, die über Telefonleitungen gesendet wurden kamen von Zeit zu Zeit nicht an.Ihnen war aufgefallen, dass die Leitungen von Zeit zu Zeit extrem rauschten. Es gab erhebliche ÜBertragungsfehler. Das war tatsächlich ein Rieseproblem.
Mandelbrot stellte die Nebengeräusche grafisch dar, und was er sah, überraschte ihn (14:48).
Für jede Zeitspanne sah das Signal immer gleich aus, wie die folgenden Filmausschnitte zeigen:
Zoom in die Struktur der Störsignale:
Ein Tag:
Eine Stunde:
Eine Sekunde:
Überblick über die Zeitspannen: Tag / Stunde / Sekunde … es sah stets gleich aus.
Das Muster war extrem selbstähnlich.
Diese Selbstähnlichkeit erinnerte Mandelbrot an ein mathematisches Rätsel, dass nahezu 100 Jahre alt war. Das Rätsel der sogenannten „Monsterkurven“.
Der deutsche Mathematiker Georg Kantor konstruierte 1883 das erste mathematische Monster mit seiner Kantormenge. Man drittel eine Strecke und entfernt den mittleren Teil. Von den übriggebliebenen 2 Strecken entfernt man wiederum den mittleren Teil und fährt dann so fort.
An jeder beliebigen Stelle des Musters findet man wieder dasselbe Muster, ähnlich des Störsignals, welches Mandelbrot bei IBM gesehen hatte.
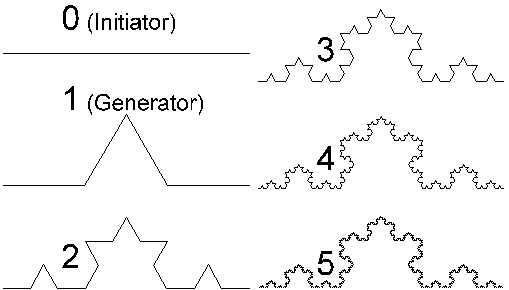
Ähnlich die Koch’sche Kurve. Für das Auge gesehen ist die Kurve absolut endlich aber mathematisch gesehen ist sie unendlich. Sie ist mit dem Maßband nicht meßbar.
Man bezeichnete diese Kurve als „pathologische Kurve“, weil es nach der euklidischen Geometrie keinen Sinn ergab.
Eine Anwendung der Kochkurve war die Bestimmung von Küstenlinien. So gab es auch einen berühmten Artikel von Mandelbrot: „Wie lang is Britanniens Küste“. Je nach Auflösung des Meßwerkzeugs ist dies unterschiedlich. Je feiner das Meßwerkzeug um so länger ist die Küste.
Dies erforderte ein Überdenken des Begriffs der Dimension. Es gab nun etwas, was zwischen 1 und 3 Dimensionen hatte. Fraktale haben sie und je rauher sie sind um so größer ist ihre fraktale Dimension, hier z.B. für einen Würfel mit D=2,895.
Ein weiteres MOnster ist die Julia-Menge. Eine Formel liefert ein Ergebnis, dass man wieder in die Formel einsetzt. Dies wiederholt man unendlich mal …
1980 Mandelbrot erschuf eine Menge, die alle Julia-Mengen in einem einzigen Bild kombinierten. f(z) = z²+c.
Dies wurde schnell ein Symbol für fraktale Geometrie: Die Mandelbrot-Menge.
Eine Kampfansage an die bisher etablierten Meinungen der Mathematik.
Die faszinierenden Bilder lösten in der Popkultur einen Trend aus. Alle wollten es haben. Als die Mandelbrot-Menge erstmals veröffentlicht wurde, reagierte der Großteil der Mathematik mit Verachtung. In einem Klatsch-Blatt für Profimathematiker behauptete ein Artikel nach dem anderen, Mandelbrot wäre überhaupt kein Mathematiker und die fraktale Geometrie wäre nutzlos.
Das Auge war aus der Naturwissenschaft „exkommuniziert“ worden.
Seine Kollegen – insbesondere die wirklich guten Theoretiker, die er respektierte, wandten sich gegen ihn. Es war ein Paradigmenwechsel. Es ist ein Zweig der Geometrie – genau, wie die euklidische Geometrie. „Viele waren der Meinung, das fraktale zwar nette aber nutzlose Bilder sein, dass aber ist lachhaft“, so Mandelbrot.
Mandelbrots Antwort war sein neues Buch: „Die fraktale Geometrie der Natur“, voller Beispiele für die Wissenschaft. Es zeigte eine völlig neue Methode, die Welt zu betrachten und zu vermessen.
Eine Anwendung der Fraktalen Geometrie war die Empfangsantenne eines Amateurfunkers, Nathen Cohen. Durch die fraktale Methode konnte die Empfangsantenne stark verkleinert werden. Die VErwendung von Fraktalen machten die Maße der Antenne nicht nur kleiner, sondern vergrößerte auch die Bandbreite der empfangenen Frequenzen:
Dies wurde erfolgreich in der HandyTechnologie umgesetzt, wo ein Gerät über mehrer Frequenzen kommunizieren kann, der Platzbedarf aber aufgrund der Handlichkeit begrenzt ist.
Warum benutzt die Natur Fraktale?
In der Natur immerwieder anzutreffen. Ein Eindrucksvolles Beispiel ist der Herzrhythmus:
Als Goldberger die Herzschläge 1000der Personen anlysierten, stellten sie fest, dass das Herz keine Maschine und kein linearer Rhytmusgeber ist.
Das Bild des Herzschlags einer gesunden Person mit einer Frequenz von 60 bis 120 Schlägen pro Minute hatte große Ähnlichkeit mit den gezackten Umrissen der in Mandelbrots abgebildeten Gebirgszüge hat.
Wenn man den Herzschlag weiter vergrößert sieht man, dass auf diesen Zacken weiter Zacken sitzen. Der gesunde Herzschlag hat also eine fraktale Architektur.
Der gesunde Herzschlag hat eine fraktale Architektur
Moderne Kardiologie. Erry Goldberger entdeckte, dass der gesunde Herzschlag ein charaktersitisches fraktales Muster hat. Eine Signat, die eines Tages Herzspezialisten helfen könnte, Herzprobleme früher zu entdecken.
Die Fraktale der Augenbewegung
Wenn das Auge auf der basis fraktaler Geometrie wahrnimmt könnte man Flugzeugcockpits, Ampelanordnungen oder andere visuelle Wahrnehmungen anders anordnen, als in linearer Weise, also einfach nebeneinander.
Diagnose auf der Basis fraktaler Analyse
Im Bereich der Krebsforschung werden ebenfalls fraktale Methode genutzt, um die Bildung von Tumoren frühzeitiger zu erkennen, indem man die feinen Netzstrukturen von Blutgefäßen auf ihre Selbstähnlichkeit oder NICHT-Selbstähnlichkeit hin untersucht.
Warum nutzen große Tiere Energie effizienter als kleine Tiere?
Geoffrey West – Institut de Santa Fe
Der Energievorteil wächst mit zunehmender Größe.Alles Leben wird durch die zugrundelegenden Netzewerke transportiert.Kreislaufsystem, Atemsystem, Nierensystem, Nervensystem – alles fraktale Strukturen.
Es wäre unheimlich uneffizient, wenn man für jede einzelne Wachstumsstufe einen neuen Satz Baupläne zu haben!! Aber wenn man einen fraktalen Code hat, der sagt, wann im Laufe der Wachstumsstufen etwas sich zu verzweigen hat, kann ein ganz einfach genetischer Code etwas produzieren, was wie ein komplizierter Organismus aussieht. Es wird mit geringem Aufwand größtmöglichen Erfolg erzielt.
Verteilung von Baumdurchmessern und Astdurchmesser sind fraktal?
Ein weitere Untersuchung erfolgte anhand eines unter Naturschutz stehende Waldstücks in Südarmerika. Dort wurde die Verteilung von Astdurchmesser, Baumdurchmessern und auch CO2-Gehalt der Blätter ermittelt. Die Forscher stellen fest, dass die Verteilung der Baumdurchmesser des gesamten Waldes der fraktalen Verteilung der Astdurchmesser eines Baumes nahezu übereinstimmt. Das ist phänomenal. Die Linie, die den Baum repräsentiert, scheint mit der des Waldes parallel zu sein.
Nachwort
Seit Generation glaubten Wissenschaftler, dass sich die Wildheit der Natur nicht mittels Mathematik definieren lässt. Aber fraktale Geometrie führt zu einem gänzlich neuen Verständnis und enthüllt eine zugrundeliegende ORdnung, die von simplen mathematischen Regeln bestimmt wird. Dank des Vokabulars der fraktalen Geometrie, können wir jetzt wesentlich mehr lesen aus dem Buch der Natur.
Aus der Sicht der Protonen Resonance
Wenn wir Fraktale auf der feinsten Ebene der Atome finden, so ist es nicht verwunderlich, dass sämtliche daraus aufgebauten Strukturen in der Natur ebenfalls zueinander fraktal sind.
Die Protonen Resonance liefert an der Stelle nicht nur die Grundlage für die Entwicklung selbstähnlicher Strukturen, sonder macht eine qualitative Aussage über physikalische Maße, innerhalb welcher die Selbstähnlichkeit zu finden ist. Über die Selbstähnlichkeit hinaus, bietet die Protonen Resonanz nun Möglichkeiten der konkreten Dimensionierung und líefert Aussagen zum Eigenschwingungsverhalten konkreter physikalischer Werte.